Introduction to the Normal Distribution & Empirical Rule

The Normal Distribution

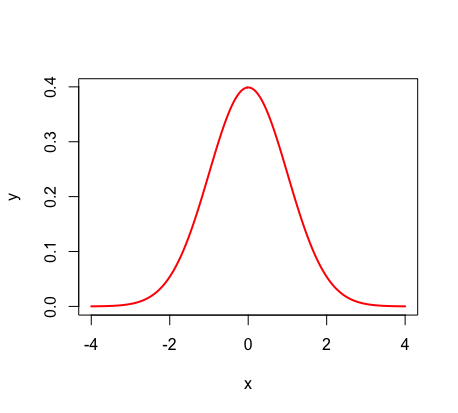
The Normal Distribution is a continuous bell shaped curve. Things such as test scores, weights, and heights can all be normally distributed.

Here are some key facts about the Normal Distribution, which is known as a Gaussian bell curve when the data is around a central value without a left or right bias:

• Usually symmetric towards the center, so 50% of the values are less than and 50% of the values greater than the mean.

• Total area under curve= 1.

• The data is most dense in the middle and less dense to the right and left.

• mean=median=mode

• Defined by mean and standard deviation:

  • mean μ -(average) expected value to measure the central tendency

  • standard deviation σ - separation used to quantify the amount of variation of a data set

The Empirical Rule

The Empricical Rule states that:

68% of data falls between one standard deviation of the mean (+/- σ) 

95% of data falls between two standard deviations of the mean (+/- 2σ)

99.7% of data falls between three standard deviations of the mean (+/- 3σ)

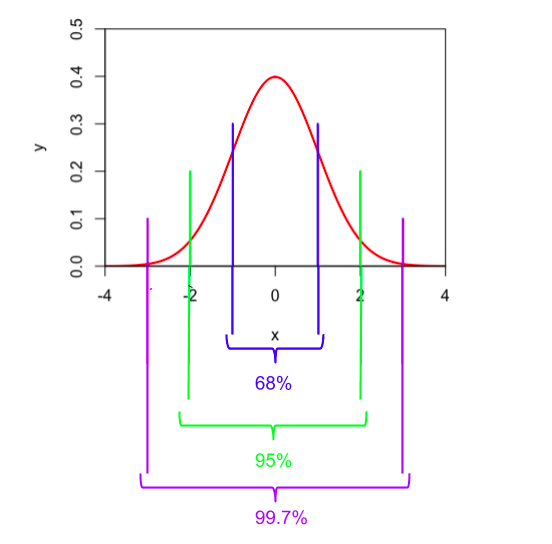
(For this distribution, the standard deviation equals one unit. In other words, σ = 1).