R: Difference of Means
Solution - part a
1. We will begin by defining the null and alternative hypthesis.
Ho: μ = μ
Ha: μ < μ
I. Hypothesis Testing - Calculating p-value Using Data
A fitness researcher
1. Enter the data into R.
# Enter x and y data
x = c(123, 91, 77, 55, 132, 109, 104, 82, 117, 93)
y = c(75, 63, 103, 103, 95, 110, 84, 114, 85, 98, 121, 107, 87, 81)
2. Let's go ahead and build side-by-side boxplot.
boxplot(x, y,
col = c("blue", "green"),
names = c("x", "y"),
horizontal = TRUE)
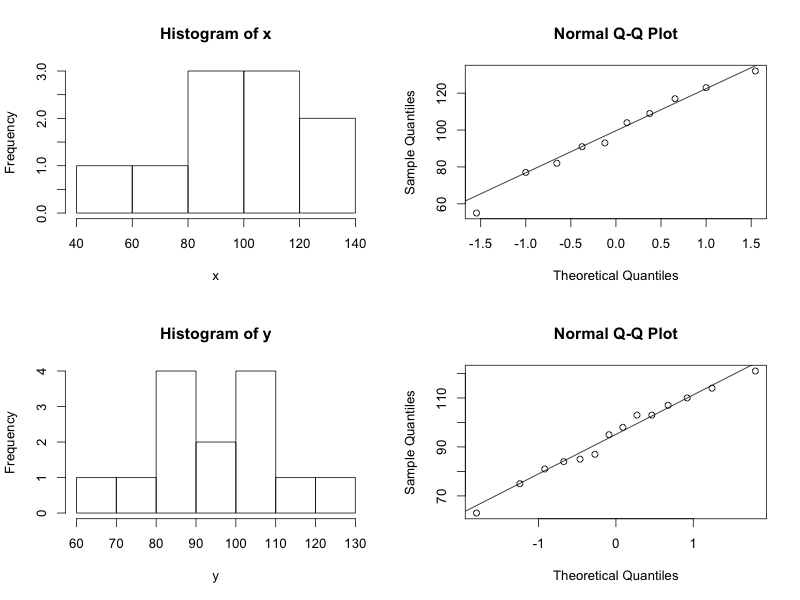
3. Lets assess normality of both the x and y variables.
# combine 4 plots into 1 to assess normality of both variables
par(mfrow=c(2,2))
hist(x)
qqnorm(x)
qqline(x)
hist(y)
qqnorm(y)
qqline(y)
SARAH.. this is the code to get numerator, denominator.. test statistic..
# summary statistics
mean.x = mean(x)
n.x = length(x)
sd.x = sd(x)
var.x = sd.x^2
mean.y = mean(y)
n.y = length(y)
sd.y = sd(y)
var.y = sd.y^2
# calculate test statistic
point.estimate = mean.y - mean.x
se = sqrt((var.x/n.x) + (var.y/n.y))
test.stat = point.estimate/se
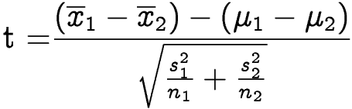
### USING JUST t.test() function .. u can get test.statistic, df, and p-value
> t.test(y, x, alternative = "less")
Welch Two Sample t-test
data: y and x
t = -0.418, df = 15.067, p-value = 0.3409
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf 11.44782
sample estimates:
mean of x mean of y
94.71429 98.30000
CONCLUSION: The p-value is 0.34.
Calculate the 90% onfidence interval.
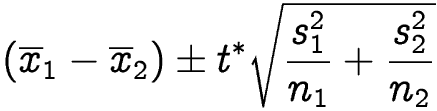
> t.test(y, x,
+ conf.level = 0.90)
Welch Two Sample t-test
data: y and x
t = -0.418, df = 15.067, p-value = 0.6818
alternative hypothesis: true difference in means is not equal to 0
90 percent confidence interval:
-18.61925 11.44782
sample estimates:
mean of x mean of y
94.71429 98.30000
Conclusion: Based on the data, I can be 95% confident that the difference in the mean of population 1 and the mean of population 2 falls between -18.62 and 11.45.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
