1. We will begin by defining the null and alternative hypthesis. 

Ho: p = 0.6

Ha: p > 0.6

2. Next, in R, will define our variables and check the conditions need for inference.

> p.hat = 47/64           # calculate sample proportion 
> p.hat
[1] 0.734375
> 
> p.null = .60            # define null proportion 
> n = 64                  # define sample size 
> 
> # Check conditions for inference
> n*p.null
[1] 38.4
> n*(1 - p.null)
[1] 25.6

Conclusion: n*phat and n*qhat are both greater than 10. Therefore, we can proceed with our inference calculations.

3. Next, we will calculate our test statistic for this problem using the following formula.

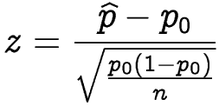
> # Calculate test statistic
> z = (p.hat - p.null)/sqrt(p.null*(1 - p.null)/n) 
> z
[1] 2.194335

4. Finally, this is a right-sided test, so we will use the following R code to find the p-value associated with a z of 2.194. 

> # Right sided test, so calculate the area to the right
> p.value = pnorm(z, lower.tail=FALSE) 
> p.value
[1] 0.01410568

Conclusion: Based on our analysis, we calculated a p-value of 0.014. Therefore, we reject the null hypothesis as 0.014 is less than 0.05. The data supports the claim that over 60% of the freshman students enrolled at Dallas University own a credit card.

Solution - part b

1. To calculate a 99% confidence interval, first start by completing steps #1 - #2 above. We will be using the following formula to calculate our confidence interval.

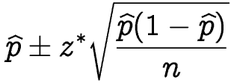
2. Once steps #1 - #2 from above are completed, we can then calculate z*, the standard error, and the margin of error as shown below:

> # Calculate z* for 90% confidence interval
> z.star = qnorm(0.95)
> z.star
[1] 1.644854
> 
> # Calculate the standard error
> se = sqrt(p.hat*(1 - p.hat)/n) 
> 
> # Calculate the margin of error
> me = z.star*(se)
> me
[1] 0.09080937

3. Now that the margin of error has been calculated. We can simply calculate the lower an upper limits of our 99% confidence interval. 

> # calculate the lower limit
> p.hat - me
[1] 0.6435656
> 
> # calculate the upper limit
> p.hat + me
[1] 0.8251844