Sampling Distributions - Proportions
I. Introduction
Think of having a perfectly fair coin, a coin that has a 50% chance of landing on heads and 50% chance of landing on tails. This proportion of 0.5 is the population proportion (i.e. the parameter). The population proportion is denoted as "p."
Now, consider if you and your friends were to flip this coin 100 times, then record the proportion of heads observed. You may observe 47 heads out 100, for a proportion of 0.47. One friend might observe 53 heads (0.53), another might observe 49 heads (0.49), etc. These various proportions are sample proportions (i.e. statistics). The sample proportion is denoted as "p̂."
If you were to graph all of those sample proportions that you and your friends observed, you would create a sampling distribution of p̂.
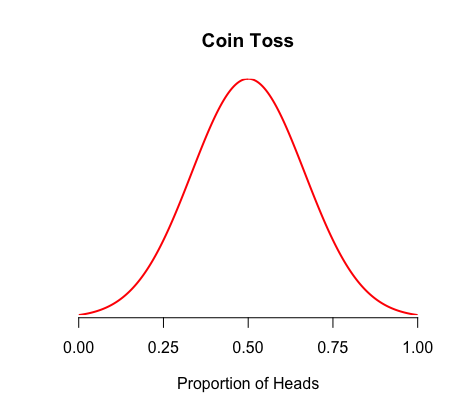
II. Mean & Standard Deviation
The mean and standard deviation of the distribution for \(\hat{p}\) is:
THE MEAN:
\(\mu_{\hat{p}} = p\)
This means that the distribution of sample proportions is centered around the population proportion. Logically, it should make sense that all of the samples you observed from tossing your coin ranged around the true proportion of 0.5.
THE STANDARD DEVIATION:
\(\sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}}\)
III. Sampling Distribution
If certain conditions are met, one can assume that the distribution of \(\hat{p}\) is approximately normal with a mean of \(p\), and a standard deviation of \(\sqrt{\frac{p(1-p)}{n}}\). The sampling distribution of \(\hat{p}\) is:
\(\hat{p} \sim N(p, \sqrt{\frac{p(1-p)}{n}})\)
CONDITIONS: The sampling distribution of \(\hat{p}\) is approximately normal if both of the following conditions are met:
\(np > 10\) & \(n(1-p) > 10\)
*For information on the Test of Independence, a concept which is related to sampling proportions, click here.
