Standard Deviation
Introduction
As mentioned previously, when comparing distributions we often are interested in calculating the mean or median to help determine the center of any particular distribution. However, once we have found an acceptable measure of center, we need a second numerical measure to measure the spread of the distribution.
EXAMPLE:
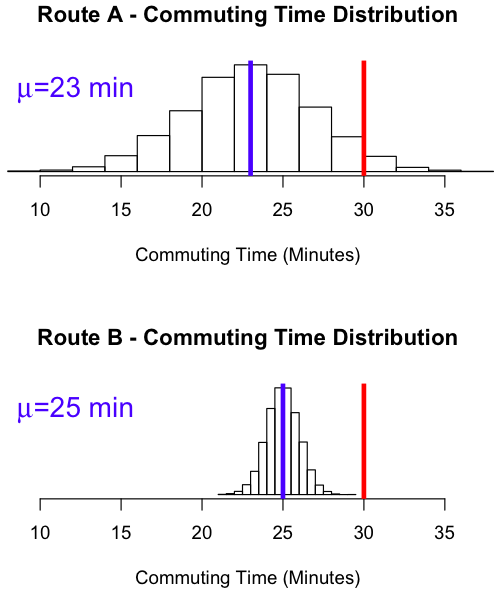
So what is the significance of spread, why is the spread important? Consider an employee who is considering two routes to work, called Route A and Route B, as shown below. The employee leaves for work every morning at 7 AM and must get to work by 7:30 AM to prevent getting in major trouble with his boss. After collecting data on the two routes, he found that Route A had a mean travel time of 23 minutes, while Route B had a mean travel time of 25 minutes, 2 minutes longer. However, while Route B was longer, the route took him through back roads with little traffic and stoplights. Route A, while on average shorter in duration, had more traffic lights that caused greater variability in his commute time. This variability was so great, that the employee found himself being late from time to time. Thus, while Route A, had a lower mean travel time, Route B was preferred due to less variability.
 |
 |
 |
Standard Deviation Formula
\(s=\sqrt{\frac{\sum (x-\overline{x})^{2}}{n-1}}\)
Variance
Variance is simply another way to measure spread. It is found by squaring the standard deviation.
\(s^{2}=\frac{\sum (x-\overline{x})^{2}}{n-1}\)
Additional Fun Facts
- When \(s\) = 0, there is no spread, and thus all the numbers are the same.
- For example, the dataset {6, 6, 6,} would have a standard deviation of zero.
- The standard deviation (\(s\)) is in the same units as the data.
Example
A student randomly samples 4 students how many hours they spent on social media the previous day. Their responses were: 2, 1, 4, 6. To calculate the standard deviation and variance from a sample, follow the following steps:
1. Calculate the mean:
\(\overline{x} = \frac{\sum x}{n}=\frac{2+1+4+6}{4}=3.25\)
2. Calculate the deviations by subtracting the mean from each individual observation:
| \(x\) | \(x-\bar{x}\) |
|---|---|
| 2 | 2 - 3.25 = -1.25 |
| 1 | 1 - 3.25 = - 2.25 |
| 4 | 4 - 3.25 = 0.75 |
| 6 | 6 - 3.25 = 2.75 |
3. Square the deviations:
| \(x\) | \(x-\bar{x}\) | \((x-\bar{x})^2\) |
|---|---|---|
| 2 | 2 - 3.25 = -1.25 | (-1.25)2 = 1.5625 |
| 1 | 1 - 3.25 = - 2.25 | (- 2.25)2 = 5.0625 |
| 4 | 4 - 3.25 = 0.75 | (0.75)2 = 0.5625 |
| 6 | 6 - 3.25 = 2.75 | (2.75)2 = 7.5625 |
4. Sum the squared deviations:
\(\sum (x-\overline{x})^{2}=1.5625+5.0625+0.5625+7.5625=14.75\)
5. Divide the sum of the squared deviations by \(n - 1\) to compute the variance:
\(s^{2}=\frac{\sum (x-\overline{x})^{2}}{n-1}=\frac{14.75}{4-1}=4.917\)
The variance is 4.917
6. To calculate the standard deviation, take the square root of variance:
\(s=\sqrt{s^{2}}=\sqrt{4.917}=2.217\) hours
The standard deviation is 2.217 hours.
